Semina/Problem Solving

Types of knowledge:

Declarative--facts and things, ie. capital of France, capital of Burkina-Faso, number of states in the union, number of states in the Commonwealth of Independent States, characteristics of rail--american, canadian, new, old. Declarative knowledge can be referenced, ie. library, databases, ask someone.

Declarative knowledge is important to problem solving, but is not problem solving by itself. College success involves declarative knowledge.

Procedural--how to, know how, skill, ie. change sparkplug, ride bicycle, juggle, tell jokes, solve problems.

All problem solving is procedural knowledge. That means, just like the other examples, problem solving is a skill, requires practice, and is related to particular contexts (ie. good jugglers are not necessarily good auto mechanics ).

Problem solving methods:

Rarely are algorithms used exclusively to solve problems. It is not really a problem if an algorithm exists, right? However, in the course of problem solving, algorithms may be applied.

Problem solving is therefore heuristic. Below we will examine several common problem solving heuristics and look at examples involving those solutions.

Problem solving heuristics:

Analogy: An analogy is when two different situations share some similarity. For example, many mathematics problems can be solved when the similarity between the current problem and a previous problem can be seen. Now consider the following problem:

Suppose you are a doctor faced with a patient who has a malignant tumor in his stomach. It is impossible to operate on the patient, but unless the tumor is destroyed the patient will die. There is a kind of ray that can be used to destroy the tumor. If the rays reach the tumor all at once at a sufficiently high intensity, the tumor will be destroyed. Unfortunately, at this intensity the healthy tissue that the rays pass through on the way to the tumor will also be destroyed. At lower intensities the rays are harmless to healthy tissue, but they will not destroy the tumor either. What type of procedure might be used to destroy the tumor with the rays, and at the same time avoid destroying the healthy tissue.

Now read this story:

A small country was ruled from a strong fortress by a dictator. The fortress was situated in the middle of the country, surrounded by farms and villages. Many roads led to the fortress through the countryside. A rebel general vowed to capture the fortress. The general knew that an attack by his entire army would capture the fortress. He gathered his army at the head of one of the roads, ready to lauch a full scale direct attack. However, the general then learned that the dictator had planted mines on each of the roads. The mines were set so that small bodies of men could pass over them safely, since the dictator needed to move his troops and workers to and from the fortress. However, any large force would detonate the mines. Not only would this blow up the road, but it would also destroy many neighboring villages. It therefore seemed impossible to capture the fortress. However, the general devised a simple plan. He divided his army into small groups and dispatched each group to the head of a different road. When all was ready he gave the signal and each group marched down a different road. Each group continued down its road to the fortress so that the entire army arrived at the fortress at the same time. In this way, the general captured the fortress and overthrew the dictator.

Few people solve this problem, but nearly all do when the second story follows the first. Interestingly, when the order of the stories is reversed, the analogy is not noticed.

Sometimes, analogies are not noticed. Consider the following statement:

Everytime I go to St. Louis, I travel by train. The problem is solve a card flipping problem in the least number of moves. The cards are illustrated below:

If each card represents a destination or a mode of travel, which cards would you have to turn over in order to determine if the rule, Everytime I go to St. Louis, I travel by train. is being followed? Why?

Now consider the following statement: Every card that has a D on one side has a 3 on the other side. Once again, we can represent the problem via four cards, as below:

Now which cards would you turn over? Why?

In the first card flipping problem, the problem is concrete and familiar. The second problem is abstract and unfamiliar. The solutions are the same, yet most people (75%) solve the first problem and only a few (4%) solve the second, regardless of the order the cards are presented.

The logical rule for solving both is: If p then q, and If not p then not q. Data like these is why we can say that familiarity and concreteness are very important to problem solving.

Subgoals: Breaking a problem up into subgoals is frequently a good strategy. The missionary and cannibals problem was an example of this heuristic. The subgoal in that problem is to get the three cannibals to the other side while the boat is on the initial side. People who are told this subgoal before they are allowed to solve the problem solve it more quickly than people who are not told the subgoal.

As an example of the subgoal heuristic, we will use the Tower of Hanoi problem. Here, the problem is to move all of your blocks from peg A to peg C with the rules that at no time can a longer block cover a shorter block, and that you may only move one block at a time.

Working backward: Start from the goal and then breakdown the problem from that end. Consider the problem of being in St. Louis at 6 p.m. Saturday. It is difficult to plan a schedule from Magnolia to St. Louis that will place you there at 6, but it is easy to plan a schedule to St. Louis from Magnolia. Assume you will be driving, and that it is 550 miles to St. Louis. If you plan to average 50 mph (includes gassing up and eating, etc.) then working backwards from St. Louis, 1800 hrs - 1100 hrs = 700 hrs, or leave Magnolia a 7: 00 a.m. If you add a stop in Little Rock, or continue the trip to Chicago with an arrival time of Monday at 9:00 a.m., then working backwards becomes even more useful. In general, the more complicated the problem, then the more useful working backward becomes. Production schedules and deliveries are routinely solved using this method.

Let’s look at the following problem: You want to paint a ladder and a ceiling green. How do you do it?

Representation: Many problems are much more easily solved when you change the way you represent the problem. Look at the following problem:

can all squares be covered by 31 dominos? Why or why not?

If you change your representation by saying that in an 31 dominos can cover 31 black squares and 31 white squares, but that we have 32 black and 30 white, then the answer is immediately obvious.

Set Change: We have already seen numerous examples of set change, here is another. Can you join the four chains below into one chain? It costs 2 cents to open a link and three cents to close a link. All links are closed at the beginning of the problem. Can you join all links for 15 cents?

Cheap necklace problem

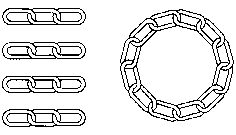
This problem is often used to illustrate incubation effects. Incubation effects occur when a problem is more easily solved after the passage of time between first seeing a problem and achieving a solution. In the cheap necklace problem, people who are interrupted and then return to the problem solve it more quickly upon returning than people who attempt to solve it without interruption.

Anagrams

kmli graus teews

recma foefce ikrdn

Functional fixedness: We have already seen some examples of functional fixedness, here are some more:

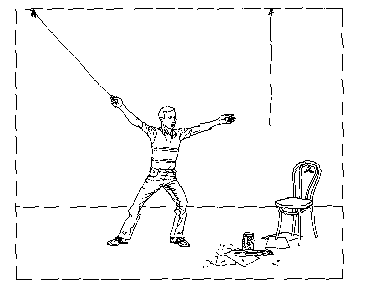
Tie the two strings together given the items shown: pins, jar, pliers, chair, paper.

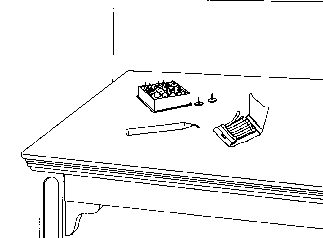
Put the candle on the back of a door, lit, using the objects shown: candle, matches, box of tacks.

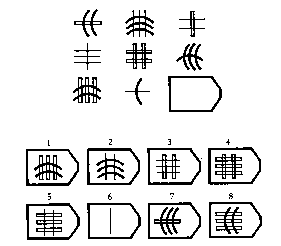
Abstract problem: which tile goes in the space provided for it above.

Take home problems:

1. The king has promised his daughter to any man who can solve the following problem. The king has three metal boxes, his daughter’s portrait is in one of those boxes. Each box has an inscription, only one inscription is true. The boxes and the inscriptions are pictured below:

Where is the picture? Tell how you know. Hint: logic is involved in solving this problem.

2. Three coins are on a table. The first and the third show tails, while the second shows heads. A move consists of turning any two coins over. How can you get the coins to show all heads or all tails?